Pursuit and Interception
Pursuit is an inherently challenging task. Chasing down and catching a small flying object is a tough problem even for humans, that’s why we tend to celebrate elite athletes who can do it reliably. Pursuit requires accuracy and speed, two things generally in direct opposition. A large portion of my work focusses on how tiny aerial hunters repeatedly catch lunch out of the air, despite having brains the size of sesame seeds.
Pursuit For Beginners:
Pocket Watches and Pirate Ships
It seems odd that these two items would have much in common, but they have both been used to lay down a theoretical framework for pursuit. The first two examples are taken from the fantastic book ‘Chases and Escapes: The Mathematics of Pursuit and Evasion’, by Paul J. Nahin. I recommend a copy to anyone interested in pretty patterns of pure mathematics.
Perrault’s Pocket Watch
In this simulation, a hand (red) drags a set of pocket watches on chains of different lengths across a table.
Around 1672, physician Claude Perrault posed a then unsolved question about motion to the polymath Gottfried Leibniz. If a watch on a chain is placed on a table, and the end of the chain dragged in a straight line, what path does the watch take? The experiment is easy; the mathematical analytical solution, harder (particularly for the time). We need not worry about this solution, but it’s worth considering that in this case, the watch is pursuing the hand that pulls the chain. However, its speed is variable and dependent on the angle of the chain. The curve made by an object dragged in this manner is called a Tractrix. It’s not important further, it’s just a cool name.
Bourguer’s Pirate Ship
In this simulation, a merchant ship (red) is chased by pirate ships travelling at different speeds.
In 1732, mathematician Pierre Bouguer laid down a hypothetical case in which a pirate ship sets to attacking a passing merchant. In this case, the pirate ship is always pointed directly toward the merchant’s. The question proposed, and solved, was: For a given speed, what path does the pirate take towards his quarry? This is closer to the problem encountered in pursuit in real life. Chaser speed is independent of the target speed, unlike in the tractrix. When chasing a fleeing target, the pirate can only catch it when his speed is higher.
In French, the shape made is a courbe de chien and in German it’s a hundekurven. Both mean: the curve of a dog. Both share the image of a dog tailing its owner, our first connection to understanding how animals might complete pursuit tasks.
Staying in Control
Both previous examples are ways to draw the paths we would expect to find in pursuit. The problem is that this doesn’t lead us to how to steer onto a pursuit course. For this we need a steering control system. This just means a pattern of rules, or algorithm, for how to navigate onto the pursuit course. The simplest possible pursuit algorithm is as follows: if the target is on your left: turn left. If on your right: turn right. I’ve simulated that controller here, with a small delay. As you can see, it kind of works, but it’s extremely inefficient.
In this simulation a pursuer (white) turns left or right based on which side it sees the target (red) on.
Error and Response
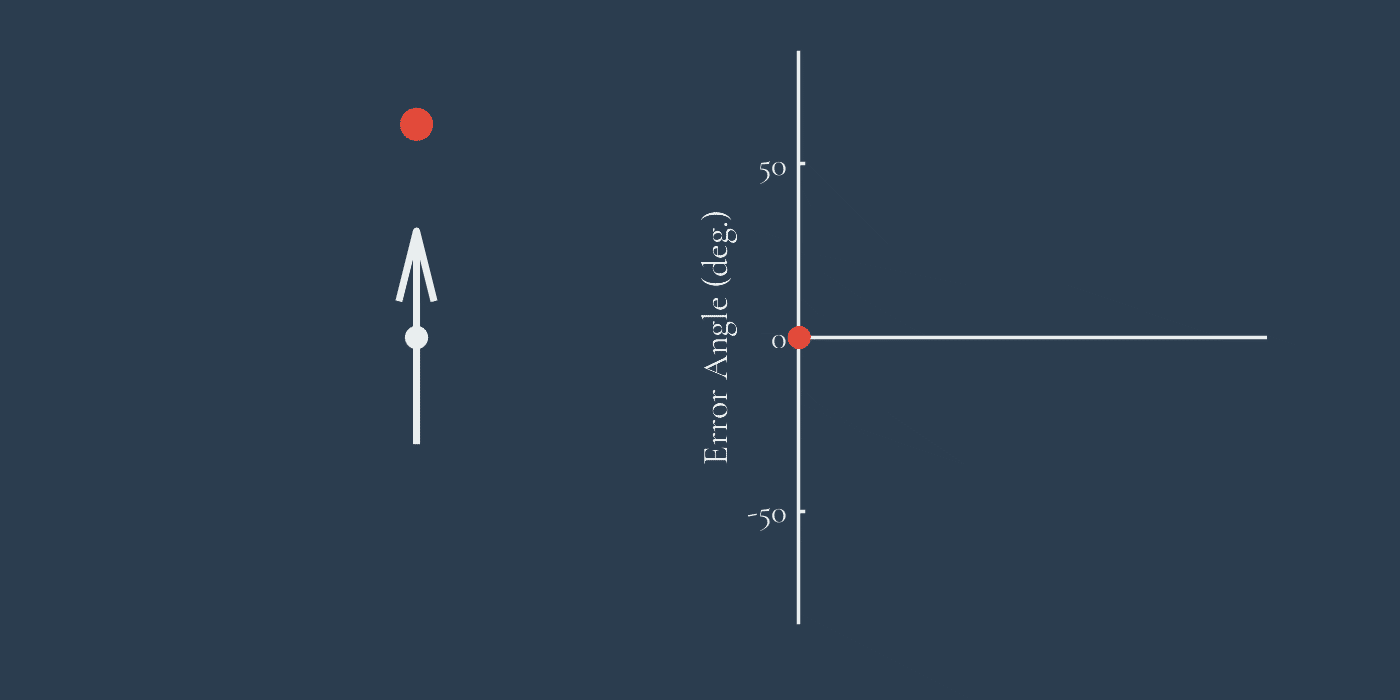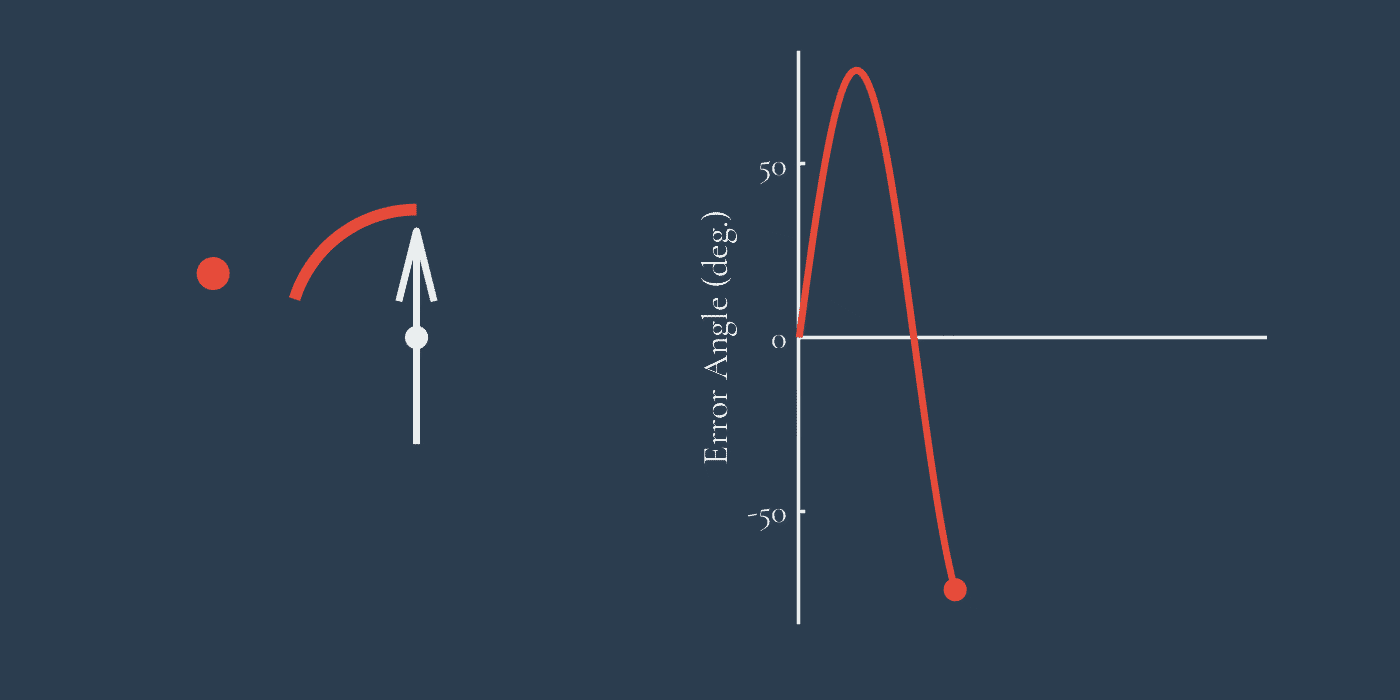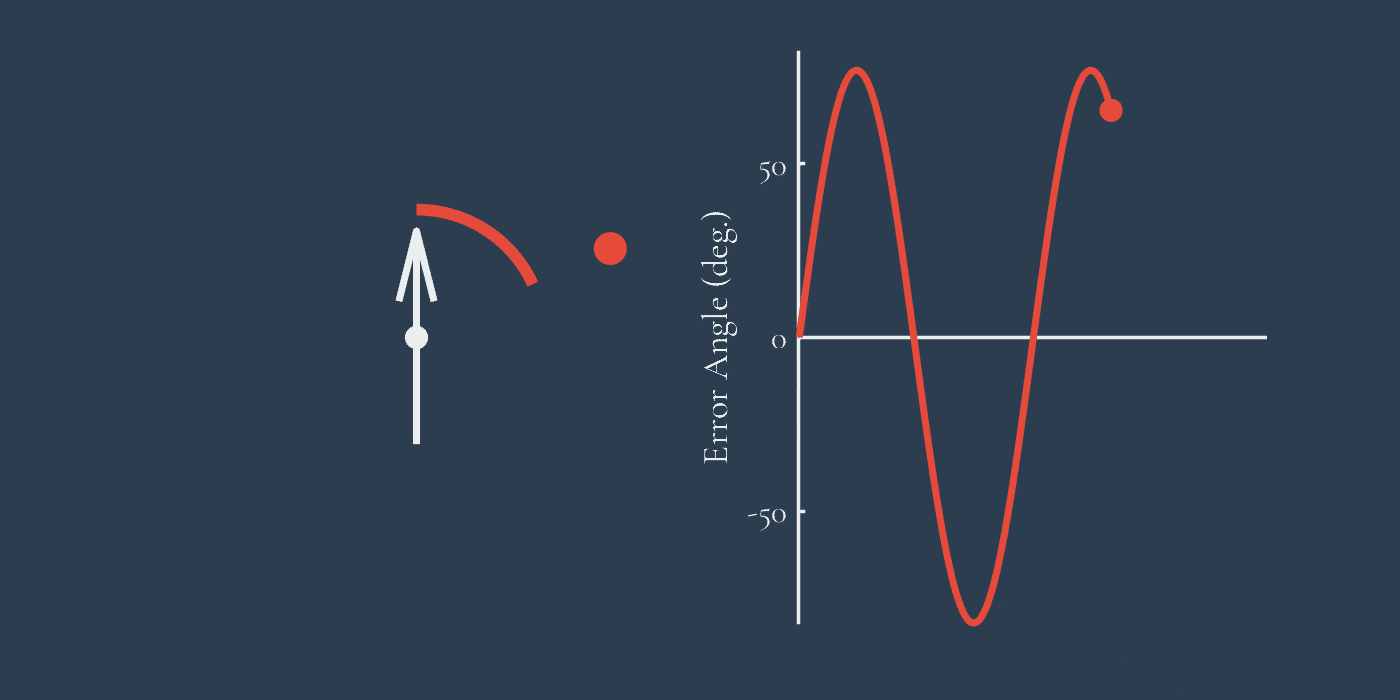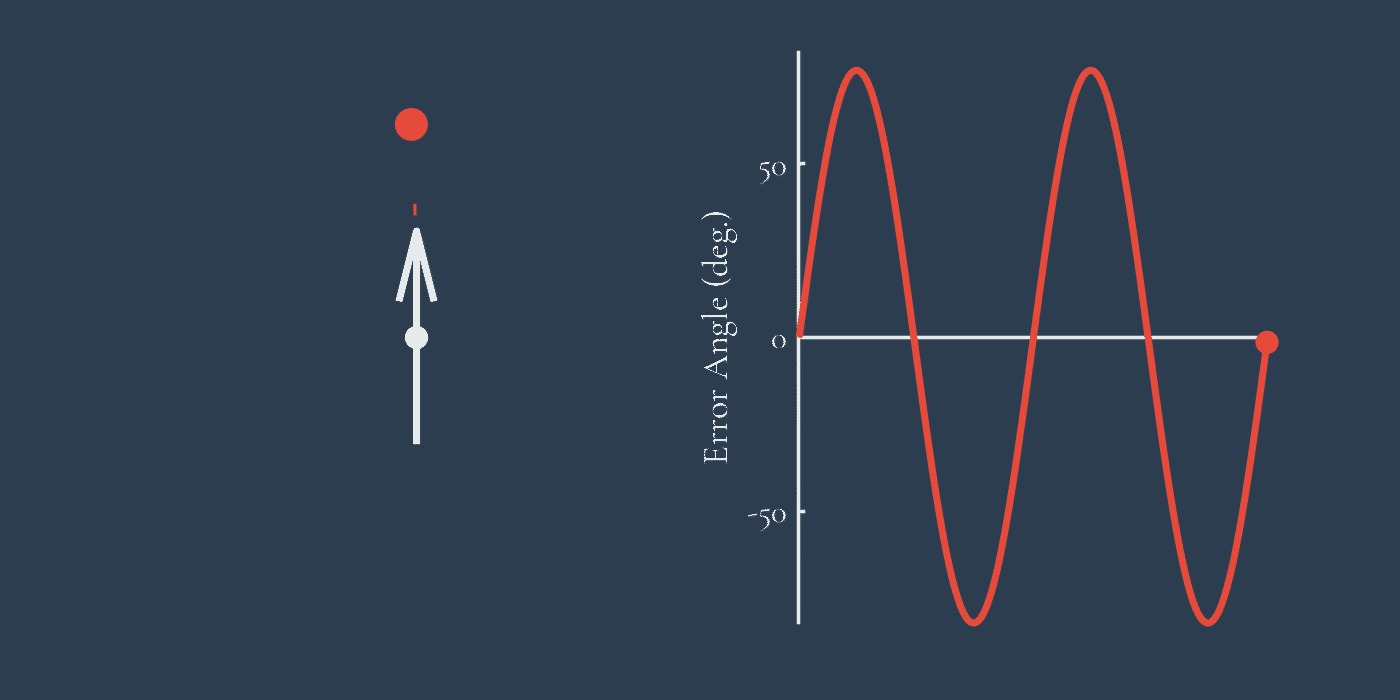
To increase our tracking efficiency, we need to change how much we steer left and right depending on how far off the target we’re currently pointing. We can represent this error as the angle between our current heading and the target, conveniently called the error angle. I’ve plotted this here to show how the error angle is measured.
We can change how much we are steering in relation to the size of the error angle. If we make this a linear relationship, then for double the error angle, we get double the turning response. This is the central idea behind proportional control, a central part of modern engineering and the model put forward for housefly chasing by Land and Collett in their seminal 1974 paper . The amount we turn, for each degree of error, is the slope’s gradient. This represents the gain constant of the controller. The units of this gain are ‘/s’, meaning that, at a gain of 5 /s, we turn at a rate 5 times the error angle per second. Higher gains result in more dramatic steering responses to correct an error angle.
Gain
Now, we’ll implement that control into our chasing simulation but with a range of different gains. As you can see, the performance is much improved. The chaser takes a smooth curve in towards the target, much like a dog following its master. All this, simply by turning in proportion to the current error in heading. However, you’ll notice that different gains result in different trajectories, even though they’re all following the same underlying pattern.
Here we have two arrows that are tracking the red target. However, they are doing so with different gains (the slope of their turning response, relative to the error angle). This effectively changes responsiveness: higher gains are more responsive. This is why the low-gain arrow seems to trail the target.
Sensory Delay
So why are gains not always maximized? There are few different answers, but one key explanation are sensory delays. There’s an inherent neural delay between an animal’s sensory measurements, and it’s actions. Delays degrade the performance of a pursuer, as demonstrated in this simulation.
High gains combined with sensory delays can also lead to overshooting, causing the pursuer to oscillate behind the target rather than simply pursue it. This interaction is referred to as damping. For a given delay, there is an optimal gain at which the chasing system is critically damped. Chasing tiger beetles are a good example of a critically damped chasing system. However, a gain lower than this is an overdamped system, and a higher gain is underdamped. The simulation here shows the characteristics of critical, over- and underdamped systems
Leading the Target
So far I’ve described the theory behind chasing the current location of the target. However, it would be more efficient for us, the predators, to head to the target’s future location. To find out how we might do this, click the button below to find out about interception.